How to calculate the inductance of a simple coil?
-
The self-inductance of a simple coil can be competed from the total magnetic energy stored in the field for a known current intensity going through the coil.
The magnetic field can be computed using one of the MagnetoStatic LF solvers (BiotSavart if possible, Vector Potential if there are metal or ferrite objects that need to be accounted for).
With these solvers, the coil has to be modeled as a filament (because only one-dimensional wires can be used as current sources). For a complete example, please follow the Tutorial "3.2.6 Self-Inductance of Qi Transmit Coil".
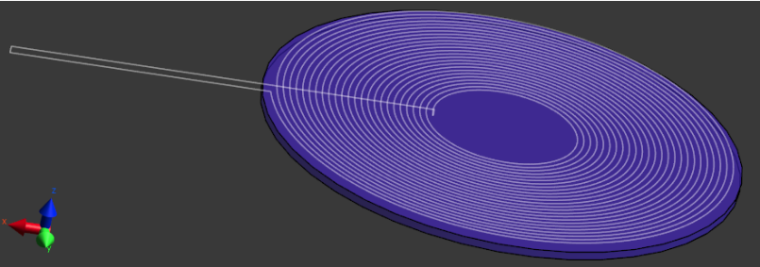
-
The mutual inductance of two (or more) coils can also be calculated by evaluating the magnetic energy. First, the inductances L1 and L2 of each coil have to calculated independently. Then, a third simulation has to be run with the currents I1 and I2 in the coils. The mutual inductance M can then be evaluated from
M = (W - 0.5 * L1 * I1 * I1 - 0.5 * L2 * I2 * I2) / (I1 * I2).
W is the total magnetic energy of the field of the two coils. It is not always obvious what the signs of the currents in the two coils should be. Therefore, it is recommended to run two simulations with two different values (or signs) for, e.g., I2. The two results for M must be identical. Otherwise, changing the sign of one of the currents should help.
-
Hi Andreas.
Since Sim4Life does not consider the secondary induced fields (the magnetic fields created when a secondary current is induced in a loop different from the source current) I was wondering if that formula for the mutual inductance is still valid. Wouldn't the magnetic energy in the domain be equal to the summation of the magnetic energies created by the two coils independently?
Thanks -
The formula above IS correct, as there are no "secondary" currents in that case. Indeed, both coils are excited, with currents I1 and I2, respectively. In that setup, the 2 coils are not independent since they act as boundary conditions one for the other. If they were independent, the mutual inductance would be zero and you can check with a small example that this is not the case here.
-